Information Theory and Coding > Entropy > Average Information Content of Symbols

Average Information Content of Symbols in Long Independence Sequences

Suppose that a source is emitting one of M possible symbols s₁, s₂ ….. s_M in a statically independent sequence. Let p₁, p₂, …….. p_M be the probabilities of occurrence of the M-symbols respectively. Suppose further that during a long period of transmission a sequence of N symbols have been generated.

On an average –

    S₁ will occur NP₁ times

    S₂ will occur NP₂ times

    ……..

   S_i will occur NP_i times

The information content of the i-th symbol is I(S_i ) = - log P_i  bits

NP_i occurrences of s_i contributes an information content of  -NP_i log P_i  bits

     Average information content per symbol H = sum (-P_i log P_i  )  i= 1,2 …M

 

     Average information content of sequence  H = sum (-P_i NP_i log p_i  )  i= 1,2 …M

Average information content per symbol is also called the source entropy

Example:

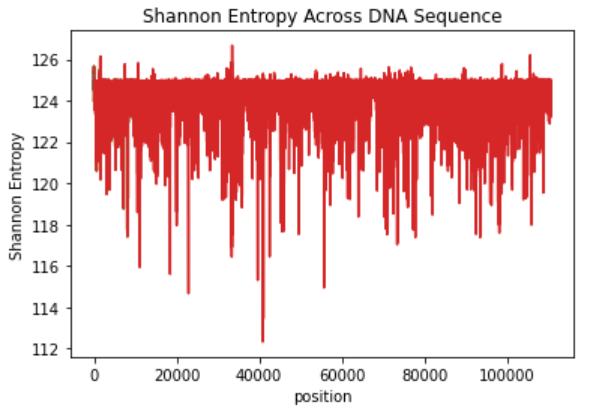
Suppose we have a DNA sequence and interested to know which area in the chromosome is more or less "surprising" and have higher information content. The following is DNA sequence and first we will consider first segment of 20 nucleotides.

ACGTACGTAACCATGACTACTACAGGGTACTACA ….. ATGCSCATGTTGGACCA

Relative frequency of A is P(A)=7/20, P(C)=6/20, P(G)=3/20 and P(T)=4/20

Average information content per symbol H = - sum[ P_i * log₂P_i ]; i=A,C,G,T

Average information content of sub-sequence  H = - sum[NP_i * P_i * log₂P_i ] i= 1,2 …M

Repeat for next sub-sequence until End:

1. Select next sub-sequence by shifting 5 nucleotides and calculate Average information content of sub-sequence H
2. Plot H against sub-sequence number

We will get the following like graph

 

 

Prev

What is entropy in Information Theory?

Next

What is Information rate?

Feedback

Submit