Information Theory and Coding > Error Control Coding > Encoding and decoding the cyclic Code: Non-Systematic Encoding

Decoding

r(x) as received polynomial, c(x) as the encoded polynomial, g(x) to be generator polynomial, and e(x) as error polynomial.

The error involved during transmission, called Syndrome, its polynomial is calculated by

So if the obtained remainder is 0 then there will be no error and if the obtained remainder is not 0 then there will be an error that needs to be corrected on the basis of the amount of reminder. The following table is the list of reminder and error position and type. The Syndrome table is as follows:

Error Code	Error Polynomial e(x)	Error pattern S(x)
1000000	1	1
0100000	x	X
0010000	X2	X2
0001000	X3	X+1
0000100	X4	X2+X
0000010	X5	X2+X+1
0000001	X6	X2+1

 

Example:

Consider decoding when the codeword c=(1100101) belonging to the (7,4) code, incurs the error and received codeword is r=(1100111)  and the generator polynomial is given  g(x) = 1+ x + x³ . Find the codeword c=(1100101)

 

Solution:

Codeword c=(1100101)  => polynomial that should be received  c(x)= 1+x+x⁴+x⁶

Codeword received r=(1100111) and received polynomial is 1+x+x⁴+x⁵+x⁶

r(x) = c(x) + e(x)

Decoding:

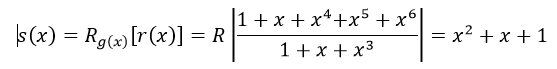
From the syndrome polynomial table error polynomial is e(x) = x⁵ for s(x)=x²+x+1

r(x) = c(x) + e(x)

c(x)= r(x) - e(x) = 1+x+x⁴+x⁵+x⁶ - x⁵ = 1+x+x⁴+ x⁶

So the corrected codeword after decode = 1100101

Prev

Encoding the cyclic Code: Non-Systematic Encoding

Next

Binary Convolutional Codes

Feedback

Submit