Information Theory and Coding > Entropy > What is data processing inequality?

Random variables X, Y, Z are said to form a Markov chain in that order (denoted by X → Y → Z) if the conditional distribution of Z depends only on Y and is conditionally independent of X. i.e.

p(x, y, z) = p(x) p(y|x) p(z|y)

 

If X and Z are conditionally independent given Y. Markovity implies conditional independence because

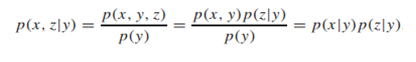
X → Y → Z if and only  p(x, z|y) = p(x|y)p(z|y)

Hence

If X → Y → Z, then it can be prove that I (X; Y ) ≥ I (X;Z) – this inequality is called data-processing inequality. This inequality can be used to show that no clever manipulation of the data can improve the inferences that can be made from the data.

By the chain rule, we can expand mutual information in two different ways

I (X; Y,Z) = I (X;Z) + I (X; Y|Z) =  I (X; Y,Z) = I (X;Z) + I (X; Y|Z)

 

Since X and Z are conditionally independent given Y, we have I (X;Z|Y ) = 0. Since I (X; Y|Z) ≥ 0, we have

I (X; Y ) ≥ I (X;Z)

 

We will have equality

if and only if I (X; Y|Z) = 0  i.e., X → Z → Y forms a Markov chain.

Similarly, we can prove that

I (Y ;Z) ≥ I (X;Z).

 

Prev

What is Chain Rule for Distance?

No More

Feedback

Submit