Simulation and Modelling > Introduction to probability and it's distribution > What is Random Variable?

Random Variable

A random variable is a numerical description of the outcome of a statistical experiment.

fig 1 

If you call a student from a group of students then the interested student who response may male or female. You are also interested with their sex (Male or female) then what is the possible outcome of the experiment?

S={ Male, Female} 

Let 1=Male, and 2= Female

Then the sample space will be  S={1, 2} 

Now you we can state the outcome of this this experiment using a variable X: X value may be 1 or 2 i.e. varies on different trials.

 X={1,2}

Since it's the vaue of X varies in different trial it is called random variable.

Depending on the outcome of random variable there are two types of random variable:

Discrete: A random variable that may assume only a finite number or an infinite sequence of values is said to be discrete. Examle: Let X is the number of students present in the class today then the Sample Space S={any real number from 0 to ∞}. Here X is a discrete random variable.

Continuous: If a random variable may have any value in some interval on the real number line is said to be continuous. Example: Let X is the weight of a person in kilograms Then Sample Space S={0 to ∞} i.e. values may be decimal and a lot of possible values. Here X is a continuous variable.

 

Event: 

Let there is a random experiment and S is the sample space S={......} i.e. set of outcomes. if we define certain subsets of S as special moment the occurance of those outcomes is called an event. In an experiment, there may be several events. Events may be exclussive / disjoint (no common outcomes) or some common outcomes. 

Suppose that A⊆S is a given event, and that the experiment is run, resulting in outcome s∈S .

If s∈A then we say that A occurs.
If s∉A then we say that A does not occur.

An event defines the value of the the random variable. X={Event A , Event B, Others} i.e. X={1,2, 0}

 

In case of several experiment:

When we conduct an experiment several times then we can summerise all the outcomes of randome variable e.i. using frequency table.

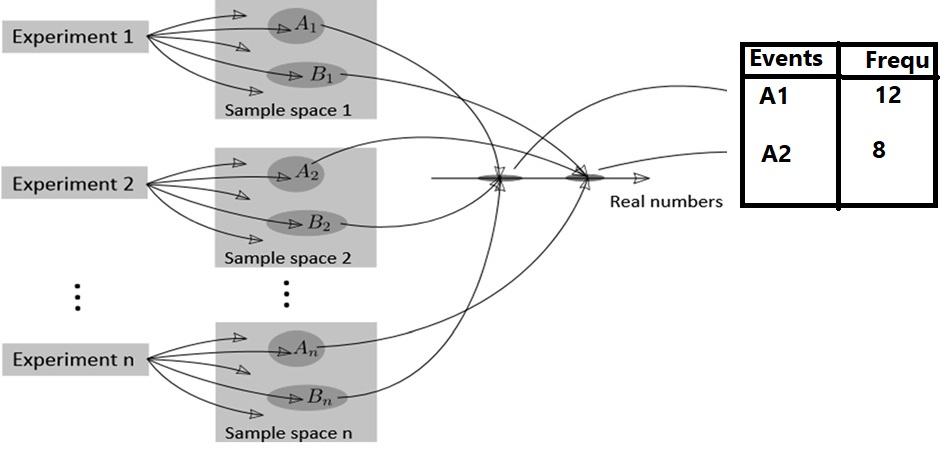
We may calculate percentages i.e. probabilities

No More

Next

What are the types of probability?

Feedback

Submit