Data Analysis Using Python > Regression > Regression Equation
Regression Equation
Regression Analysis is a technique used to estimate the relationship between variables and predict the value of one variable (dependent variable) on the basis of other variables (independent variables). This technique concerned with predicting some variables by knowing others i.e. the process of predicting variable Y using variable X’s. it tells you how values in y change as a function of changes in values of x.
Principals
Regression analysis calculates the “best-fit” line for a certain set of data. The regression line makes the sum of the squares of the residuals smaller than for any other line. Residual is the difference between actual point and predicted point on the line.
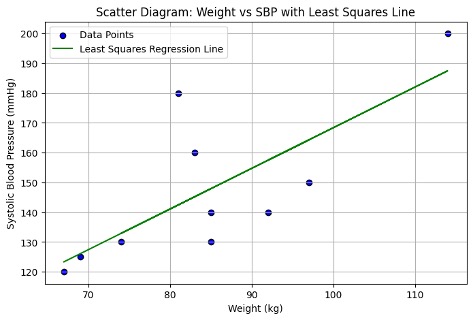Regression equation describes the regression line mathematically
- Intercept
- Slope
SBP = b0 + b1* Weight
Here observing the picture b0 can be approximated to 120 and b1 to tan(45)=1
For better understanding the equation mathematically let us understand the following picture:
Value of “a” is the portion of Y-axis cut by the line and “b” is the slope which is the tangent of angle created by the line and X-axis.
Example: The following regression equation constructed using the data where dependent is number study hours and predicted is grade in the course. What is the mathematical equation of this line?
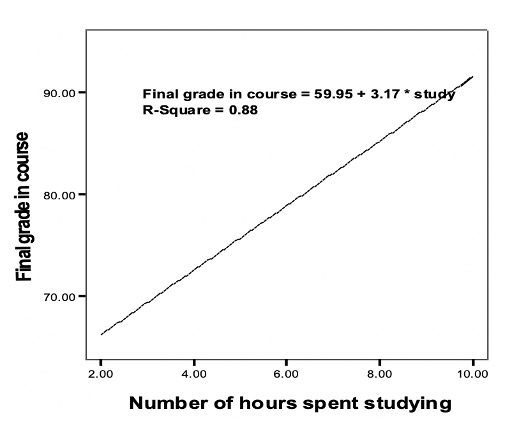
Predicted final grade in course = 59.95 + 3.17 * (number of hours you study per week)
Let us predict some grades:
- Someone who studies for 12 hours
Final grade = 59.95 + (3.17*12)
Final grade = 97.99
- Someone who studies for 1 hour:
Final grade = 59.95 + (3.17*1)
Final grade = 63.12
Feedback
ABOUT
Statlearner
Statlearner STUDY
Statlearner