Machine Learning > Sampling > What is Markov process?

A Markov Chain or Markov process is a random process in which the future is independent of the past, given the present.

Consider a collection of random variables X₀, X₁, ….., X_n . where X_n as the state of the system at time n and suppose that the set of possible values of the X_n is the set 1, …. N . If there exists a set of numbers P_ij, i, j =1,2,… N, such that whenever the process is in state i then, independent of the past states, the probability that the next state is j is P_ij, the we say that the collection {X_n, n >=0} constitutes a Markov chain having transition probabilities P_ij, I,j=1,2, ….N

 Since the process must be in some state after it leaves state I, these transition probabilities satisfy

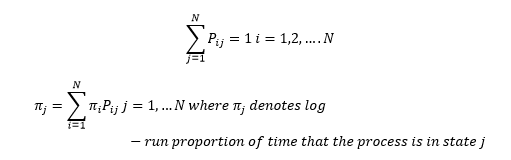
Example:

We have a restaurant that changes its menu daily. The chef is a very simple man so the only food he cooks is either fish or pasta. The choice of food he cooks can be described with the following probabilities:

P(Fish/Fish)=0.20 i.e. the probability for the chef to cook fish given the already cooked fish yesterday is 20%.

P(Fish / Pasta)=0.70

P(Pasta/Fish)=0.80

P(Pasta / Pasta)=0.30

 

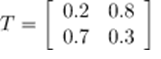
No More

Next

What is Bayesian Analysis?

Feedback

Submit