Information Theory and Coding > Entropy > Chain rule for Entropy

Chain rule for Entropy

We know that the naturalness of the definition of joint entropy and conditional entropy is exhibited by the fact that entropy of a pair of random variables is the entropy of one plus the conditional entropy of the other. i.e

 

H (X, Y ) = H (X) + H (Y|X)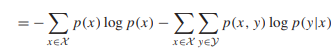

Alternatively we can write   H (X₁, X₂ ) = H (X₁) + H (X₂|X₁)  . This can be extend for X₁, X₂, X₃ as

H (X₁, X₂, X₃) = H (X₁) + H (X₂|X₁) + H (X₃|X₁, X₂)

Similarly for X₁, X₂, X₃ …. X_n joint entropy is

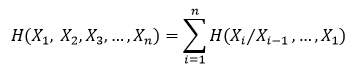
Subaditivity rule

This rule says that conditioning entropy can only reduce the entropy. However conditioning on a specific realization of B does not necessarily reduce entropy

i.e. H(A|B) = H(AB) − H(B) ≤ H(A) + H(B) − H(B) ≤ H(A)

or H(A|B) =  ≤ H(A)

 

Prev

Joint Entropy and Conditional Entropy

Next

What is relative Entropy?

Feedback

Submit