Information Theory and Coding > Entropy > What is relative Entropy?

What is Relative Entropy?

.Entropy of a random variable is a measure of the uncertainty of the random variable. It is a measure of the amount of information required on the average to describe the random variable.

Relative entropy is a measure of the distance between two distributions. Relative entropy is also called Kullback–Leibler distance.

Suppose, probability distribution of an even, which outcome is x, can be expressed using two different distribution r and s. i.e. probability function are r(x) and s(x). The relative entropy D(r||s) is a measure of the inefficiency of assuming that the distribution is r when the true distribution is s.

 For example, if we knew the true distribution r of the random variable, we could construct a code with average description length H (r). If, instead, we used the code for a distribution s, we would need H (r) + D(r||s) bits on the average to describe the random variable.

 

 

Example: Let X={0,1} and consider two distribution r and s on X. Let r(0)= 1-t, r(1)=t

and s(0)=1-k and s(1)=k

If t=k then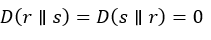

If r(1)=t=1/2 and s(1)= s =1/4 then 

 

Prev

Chain rule for Entropy

Next

What is Mitual Information?

Feedback

Submit