Information Theory and Coding > Entropy > What is Mitual Information?

Mutual Information:

Mutual information is a measure of the amount of information one random variable contains about another random variable.

Consider two random variables X and Y with a joint probability mass function p(x, y) and marginal probability mass functions p(x) and p(y). The mutual information I (X; Y ) is the relative entropy between the joint distribution and the product distribution p(x)p(y):

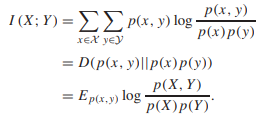
By replacing conditional probability P(AB)=P(A/B) * P(B)

 

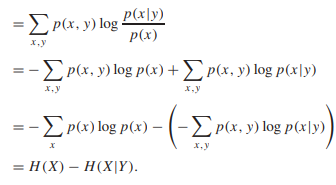
Thus, the mutual information I (X; Y ) is the reduction in the uncertainty of X due to the knowledge of Y. By symmetry, it also follows that

I (X; Y ) = H (Y ) − H (Y|X).

 Thus, X says as much about Y as Y says about X. Since H (X, Y ) = H (X) + H (Y|X), we have

I (X; Y ) = H (X) + H (Y ) − H (X, Y )

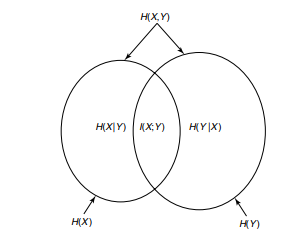
Thus, mutual information I(X; Y) corresponds to the intersection of the information in X with the information in Y.

I (X; Y ) = H (X) − H (X|Y ) = H (Y ) − H (Y|X)

We know that H(A|B) = H(AB) − H(B)

I (X; Y ) = H (X) − [ H(X,Y)-H(Y) ]=H(X)+H(Y) − H (Y|X)

Prev

What is relative Entropy?

Next

What is Chain rule of Mutual Information?

Feedback

Submit